Using ml_utils functions from the jmspack package

Showing the usage of the following ml_utils functions

• silence_stdout()

• plot_decision_boundary()

• plot_cv_indices()

• plot_learning_curve()

• dict_of_models

• multi_roc_auc_plot()

• optimize_model()

• plot_confusion_matrix()

• summary_performance_metrics_classification()

import os
tmp = os.getcwd()
os.chdir(tmp.split("jmspack")[0] + "jmspack")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from jmspack.ml_utils import (
                              plot_decision_boundary,
                              plot_cv_indices,
                              plot_learning_curve,
                              dict_of_models,
                              multi_roc_auc_plot,
                              optimize_model,
                              plot_confusion_matrix,
                              summary_performance_metrics_classification
                          )

from jmspack.utils import JmsColors
from sklearn.model_selection import (
    TimeSeriesSplit,
    KFold,
    ShuffleSplit,
    StratifiedKFold,
    GroupShuffleSplit,
    GroupKFold,
    StratifiedShuffleSplit
)

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix

os.chdir(tmp)

if "jms_style_sheet" in plt.style.available:
    _ = plt.style.use("jms_style_sheet")

df = sns.load_dataset("iris")

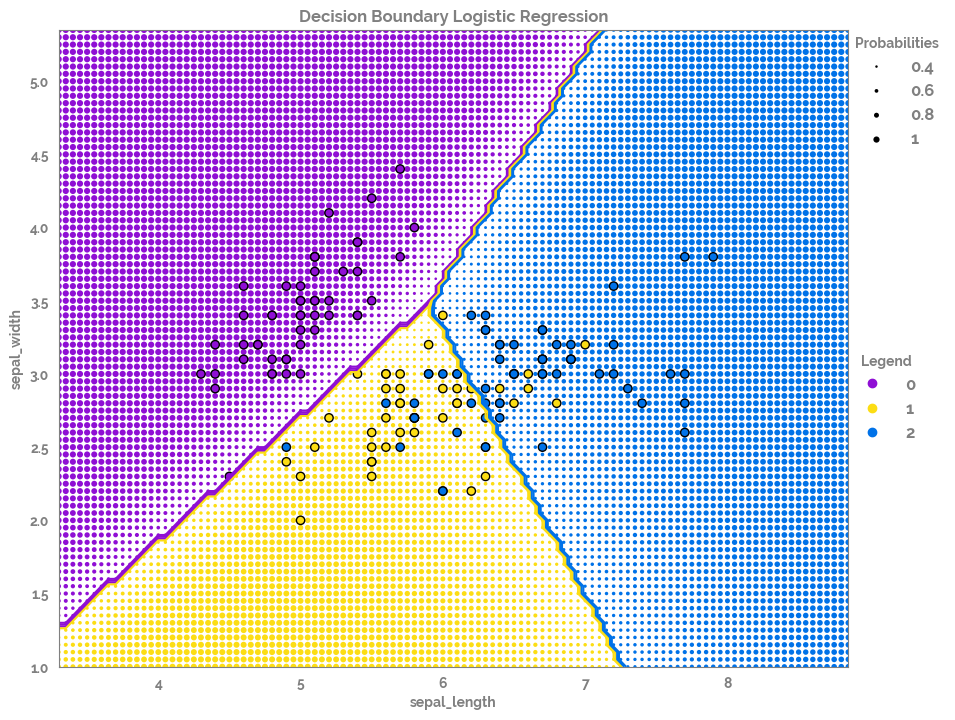
plot_decision_boundary

feature_list = df.columns.tolist()[0:2]
target = "species"
X = df[feature_list]
y = df[target]

fig, ax = plot_decision_boundary(X=X, y=y)

plot_cv_indices

n_points = X.shape[0]
n_splits = 5
uneven_groups = np.sort(np.random.randint(0, 10, n_points))

cvs = [TimeSeriesSplit,
    KFold,
    ShuffleSplit,
    StratifiedKFold,
    GroupShuffleSplit,
    GroupKFold,
    StratifiedShuffleSplit]

for cv in cvs[0:2]:
    fig, ax = plot_cv_indices(cv(n_splits), X, y.astype("category").cat.codes, uneven_groups, n_splits)

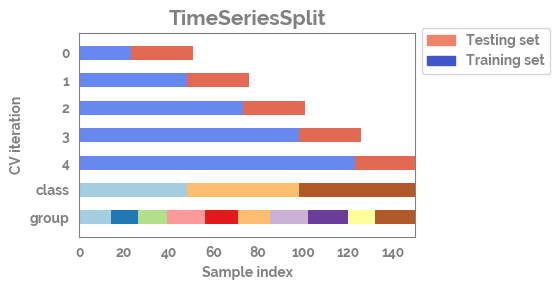
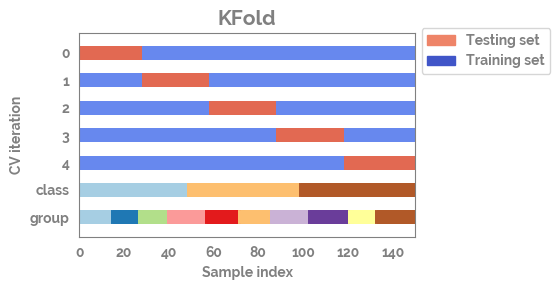
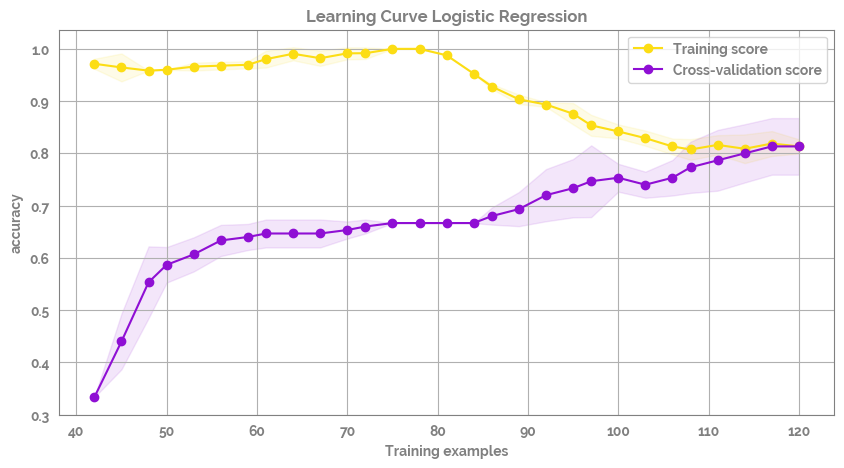
plot_learning_curve

fig, ax = plot_learning_curve(X=X, y=y.astype("category").cat.codes)

dict_of_models

dict_of_models

[{'label': 'Logistic Regression', 'model': LogisticRegression()},
 {'label': 'Gradient Boosting', 'model': GradientBoostingClassifier()},
 {'label': 'K_Neighbors Classifier',
  'model': KNeighborsClassifier(n_neighbors=3)},
 {'label': 'SVM Classifier (linear)',
  'model': SVC(C=0.025, kernel='linear', probability=True)},
 {'label': 'SVM Classifier (Radial Basis Function; RBF)',
  'model': SVC(C=1, gamma=2, probability=True)},
 {'label': 'Gaussian Process Classifier',
  'model': GaussianProcessClassifier(kernel=1**2 * RBF(length_scale=1))},
 {'label': 'Decision Tree (depth=5)',
  'model': DecisionTreeClassifier(max_depth=5)},
 {'label': 'Random Forest Classifier(depth=5)',
  'model': RandomForestClassifier(max_depth=5, max_features=1, n_estimators=10)},
 {'label': 'Multilayer Perceptron (MLP) Classifier',
  'model': MLPClassifier(alpha=1, max_iter=1000)},
 {'label': 'AdaBoost Classifier', 'model': AdaBoostClassifier()},
 {'label': 'Naive Bayes (Gaussian) Classifier', 'model': GaussianNB()},
 {'label': 'Quadratic Discriminant Analysis Classifier',
  'model': QuadraticDiscriminantAnalysis()}]

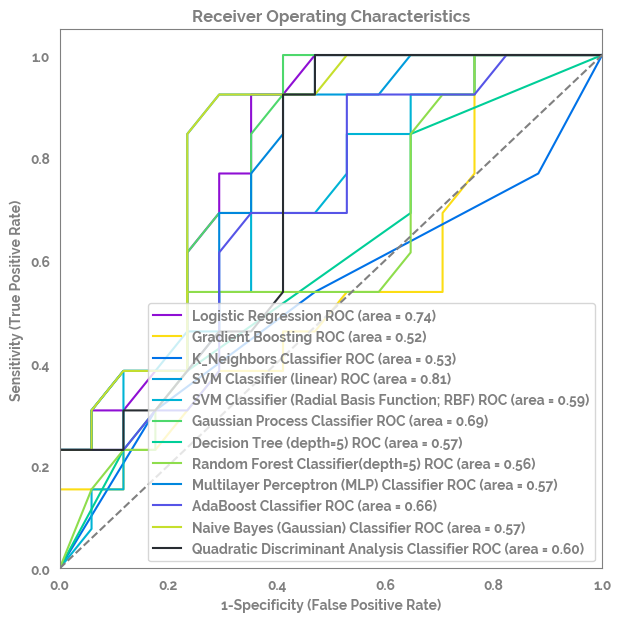
multi_roc_auc_plot

X = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), feature_list]
y = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), target]

fig, ax = multi_roc_auc_plot(X=X, y=y.astype("category").cat.codes)

optimize_model

feature_list = df.columns.tolist()[0:4]
X = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), feature_list]
y = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), target].astype("category").cat.codes

(optimized_estimator,
 feature_ranking,
feature_selected,
feature_importance,
 optimal_params
) = optimize_model(X=X, y=y)

Fitting estimator with 4 features.
Fitting estimator with 3 features.

- Sizes :
- X shape = (100, 4)
- y shape = (100,)
- X_train shape = (70, 4)
- X_test shape = (30, 4)
- y_train shape = (70,)
- y_test shape = (30,)

- Model info :
- Optimal Parameters = {'bootstrap': True, 'ccp_alpha': 0.0, 'class_weight': None, 'criterion': 'gini', 'max_depth': 1, 'max_features': 'log2', 'max_leaf_nodes': None, 'max_samples': None, 'min_impurity_decrease': 0.0, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'n_estimators': 40, 'n_jobs': None, 'oob_score': False, 'random_state': None, 'verbose': 0, 'warm_start': False}
- Selected feature list = ['sepal_length', 'petal_length']
- Accuracy score on test set = 86.7%

optimal_params

	bootstrap	ccp_alpha	class_weight	criterion	max_depth	max_features	max_leaf_nodes	max_samples	min_impurity_decrease	min_samples_leaf	min_samples_split	min_weight_fraction_leaf	n_estimators	n_jobs	oob_score	random_state	verbose	warm_start
optimal_parameters	True	0.0	None	gini	1	log2	None	None	0.0	1	2	0.0	40	None	False	None	0	False

plot_confusion_matrix

clf = LogisticRegression()
X = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), feature_list]
y = df.loc[df[target].isin(df[target].unique().tolist()[1:3]), target].astype("category").cat.codes

train_set_percentage = 0.6
train_X = X.sample(frac=train_set_percentage, random_state=69420)
train_y = y.loc[train_X.index]
test_X = X.drop(train_X.index, axis=0)
test_y = y.drop(train_X.index, axis=0)

_ = clf.fit(X = train_X,
            y = train_y)

pred_y = clf.predict(test_X)
cf_matrix = confusion_matrix(test_y, pred_y)

fig, ax = plot_confusion_matrix(cf=cf_matrix, title="Confusion Matrix classifying flower species")

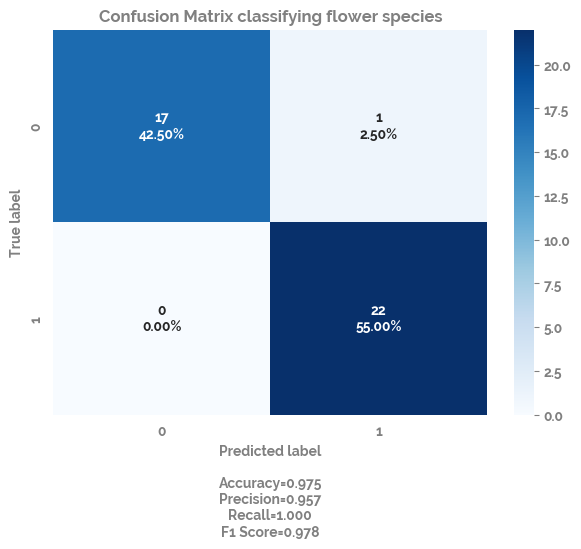
summary_performance_metrics_classification

metrics_df = summary_performance_metrics_classification(model=clf, X_test=test_X, y_true=test_y)
metrics_df

	TN	FP	FN	TP	Accuracy	Balanced Accuracy	Prevalence	Sensitivity	Specificity	PPV	NPV	auc	Mean AUC (CI 5%-95%)	F1
scores	17	1	0	22	0.975	0.972	0.55	1.0	0.944	0.957	1.0	0.995	0.995 (95% CI 0.995-0.995)	0.978